| François Labelle & computer |
| Retros mailing list, January 19, 2004 |

|
|
Proof game in 3.5 moves (2004 solutions) |
Chess positions are more tricky to define than chess games. I can see at least 4 possible definitions:
As you can see many definitions are possible. This page discusses definitions 2 and 1 (in this order).
Note that neither "position" nor "diagram" has a standard definition in chess literature, so when you read something outside of this page you should focus on the intent and not on the actual word used. For example, chess problems are implictly problems about what I call diagrams because castling and en passant information is missing. Recovering this information is sometimes even the problem!
A chess position is "uniquely realizable" if there is only one chess game that leads to the position in the specified number of plies.
| uniquely realizable | all | |
|---|---|---|
| ply 0 | 1 | 1 |
| ply 1 | 20 | 20 |
| ply 2 | 400 | 400 |
| ply 3 | 1862 | 5362 |
| ply 4 | 9825 | 72078 |
| ply 5 | 53516 | 822518 |
| ply 6 | 311642 | 9417681 |
| ply 7 | 2018993 | 96400068 |
| ply 8 | 12150635 | 988187354 |
| ply 9 | 69284509 | 9183421888 |
| ply 10 | 382383387 | 85375278064 |
| ply 11 | 1994236773 | 726155461002 |
A chess diagram is "uniquely realizable" if there is only one chess game that leads to the diagram in the specified number of plies. In the language of chess problems, these are called dual-free proof game problems. A "proof game" is a legal (though possibly weird) chess game reaching a given diagram, thereby proving that the diagram is legal (reference). A chess problem must usually be dual-free (have a unique solution) to be considered for publication.
| uniquely realizable | all | |
|---|---|---|
| ply 0 | 1 | 1 |
| ply 1 | 20 | 20 |
| ply 2 | 400 | 400 |
| ply 3 | 1862 | 5362 |
| ply 4 | 9373 | 71852 |
| ply 5 | 51323 | 815677 |
| ply 6 | 298821 | 9260610 |
| ply 7 | 1965313 | 94305342 |
| ply 8 | 11759158 | 958605819 |
| ply 9 | 66434263 | 8866424380 |
| ply 10 | 365037821 | 81766238574 |
| ply 11 | 1895313862 | 692390232505 |
Sometimes a diagram with multiple solutions can be fun:
| François Labelle & computer |
| Retros mailing list, January 19, 2004 |

|
|
Proof game in 3.5 moves (2004 solutions) |
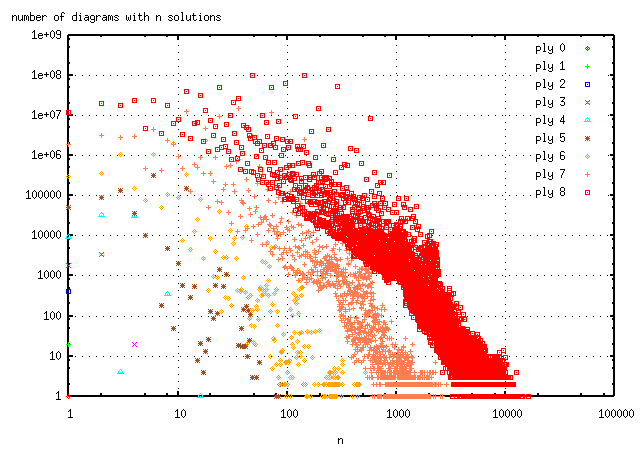
Which values of n can be obtained in this way? I know the answer for plies 0-10. A summary is given in the table and graph below. It may seem that we can eventually cover all the integers by increasing the ply count, but in 2005 I showed by a counting argument that there exists an n that cannot be obtained no matter the number of plies. In 2014, FIDE introduced the 75-move rule which made chess finite, leading to a simpler proof of the result.
| largest n with a diagram | lowest n without a diagram | |
|---|---|---|
| ply 0 | 1 | 2 |
| ply 1 | 1 | 2 |
| ply 2 | 1 | 2 |
| ply 3 | 4 | 3 |
| ply 4 | 16 | 5 |
| ply 5 | 91 | 25 |
| ply 6 | 524 | 93 |
| ply 7 | 2899 | 679 |
| ply 8 | 16327 | 3413 |
| ply 9 | 135024 | 23993 |
| ply 10 | 1351762 | 173609 |
| ply 11 | 14538568 | 930853 |
A chess diagram is called "at home" if all the surviving pieces are apparently on their start squares (aka "deletion", "chez soi"). See Homebase proof games for many examples. Click on a number in the table below to access a file with the diagrams.
| uniquely realizable | with 2 solutions | all | |
|---|---|---|---|
| ply 0 | 1 | 0 | 1 |
| ply 1 | 0 | 0 | 0 |
| ply 2 | 0 | 0 | 0 |
| ply 3 | 0 | 0 | 0 |
| ply 4 | 0 | 0 | 1 |
| ply 5 | 0 | 0 | 0 |
| ply 6 | 0 | 0 | 0 |
| ply 7 | 0 | 0 | 9 |
| ply 8 | 10 | 12 | 74 |
| ply 9 | 41 | 30 | 255 |
| ply 10 | 116 | 187 | 1350 |
| ply 11 | 335 | 512 | 4719 |
| ply 12 | 1111 | 1522 | 18535 |
| ply 13 | 2619 | 3599 | 58489 |
| ply 14 | 6067 | 9286 | 189876 |
| ply 15 | 12788 | 21063 | 548129 |
| ply 16 | 26692 | 44999 | 1550081 |
The symmetry considered here is horizontal symmetry with black and white interchanged. See Asymmetric play to symmetric diagrams for some examples. Click on a number in the table below to access a file with the diagrams. Note that an odd ply guarantees asymmetric solutions.
| with 1 symmetric solution | with 2 symmetric solutions | with 1 asymmetric solution | with 2 asymmetric solutions | with 1 of each | all | |
|---|---|---|---|---|---|---|
| ply 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| ply 1 | 0 | 0 | 0 | |||
| ply 2 | 20 | 0 | 0 | 0 | 0 | 20 |
| ply 3 | 8 | 0 | 8 | |||
| ply 4 | 85 | 0 | 0 | 0 | 0 | 260 |
| ply 5 | 8 | 11 | 177 | |||
| ply 6 | 372 | 0 | 0 | 0 | 6 | 2816 |
| ply 7 | 9 | 8 | 2392 | |||
| ply 8 | 1243 | 0 | 12 | 104 | 17 | 26925 |
| ply 9 | 53 | 109 | 25843 | |||
| ply 10 | 3723 | 27 | 110 | 467 | 163 | 232380 |
| ply 11 | 685 | 1398 | 241868 | |||
| ply 12 | 12327 | 134 | 691 | 1698 | 897 | 1826345 |
| ply 13 | 3999 | 5772 | 2045254 | |||
| ply 14 | 34353 | 442 | 12366 | 9125 | 3415 | 13226846 |
| ply 15 | 15084 | 25330 | 15787105 |
The title says it all: the diagram shows a checkmate. Actually it's more tricky than it looks: checkmate is a property of "position", not diagram, and it is possible for the same diagram to be checkmate or not checkmate depending on what the last move was. For example:

So technically in the table below (column "all") I'm counting diagrams that are checkmate for at least one game in the specified number of plies. For diagrams that have exactly 1 checkmate solution, I check that the diagram cannot be realized in any other (non-checkmate) way. François Perruchaud showed that the test can fail at ply 13: there is only one way to reach the diagram above in 6.5 moves with checkmate (1.e3 h5 2.Bc4 h4 3.Bxf7+ Kxf7 4.Qf3+ Kg6 5.Qf4 Kh5 6.g3 g6 7.g4#), but the diagram is not uniquely realizable because there are 4 other ways to reach the diagram in 6.5 moves without checkmating (for example 1.e3 h5 2.Bc4 h4 3.Bxf7+ Kxf7 4.Qf3+ Kg6 5.Qe4+ Kh5 6.Qf4 g6 7.g4+). Later I found more examples by computer, including 3 shorter ones in 12 plies.
Click on a number in the table below to access a file with the diagrams.
| with 1 checkmate solution | with 2 checkmate solutions | all | ||
|---|---|---|---|---|
| uniquely realizable | not uniquely realizable | |||
| ply 0 | 0 | 0 | 0 | 0 |
| ply 1 | 0 | 0 | 0 | 0 |
| ply 2 | 0 | 0 | 0 | 0 |
| ply 3 | 0 | 0 | 0 | 0 |
| ply 4 | 0 | 0 | 4 | 4 |
| ply 5 | 3 | 0 | 38 | 105 |
| ply 6 | 51 | 0 | 25 | 1251 |
| ply 7 | 1106 | 0 | 1513 | 26542 |
| ply 8 | 3813 | 0 | 5797 | 212907 |
| ply 9 | 47300 | 0 | 82349 | 3555181 |
| ply 10 | 216420 | 0 | 363361 | 25410051 |
| ply 11 | 2057581 | 0 | 3735018 | 340122090 |
| ply 12 | 10276981 | 3 | 21039750 | 2355723056 |
| ply 13 | 74358924 | 43 | 150292121 | 26514174333 |
Often a diagram is achievable in p plies, but in no fewer plies. In that case, a game reaching the diagram in p plies is called a "shortest proof game". In the table below, the column "uniquely realizable" therefore counts the number of dual-free shortest proof game problems. The column "all" is also interesting because each legal diagram appears exactly once in it (indexed by the length of its shortest proof game(s)). This means that the counts in that column eventually drop to zero, and their sum is equal to the number of legal diagrams. As noted on the parent page, the count is known to be non-zero for ply 366.
| uniquely realizable | all | |
|---|---|---|
| ply 0 | 1 | 1 |
| ply 1 | 20 | 20 |
| ply 2 | 400 | 400 |
| ply 3 | 1702 | 5202 |
| ply 4 | 8659 | 69731 |
| ply 5 | 49401 | 766337 |
| ply 6 | 287740 | 8708079 |
| ply 7 | 1934794 | 86540204 |
| ply 8 | 11569093 | 880526165 |
| ply 9 | 65443733 | 7996545696 |
| ply 10 | 360231372 | 73802185449 |
| ply 11 | 1872156836 | 616052245142 |
Diagrams that have a shorter realization can also be interesting. They are especially interesting if the diagram is uniquely realizable in p plies. Imagine the frustration when you're asked for a proof game in p plies, and you can easily do it in fewer plies but the solution in exactly p plies eludes you! One must find a way to waste moves, also called "losing tempo".
The table below counts diagrams that have a unique realization in p plies, but where the shortest possible realization is in p − t plies, where t > 0 is the tempo achieved. The table can be thought of as a breakdown of the numerical difference between the "uniquely realizable" columns from sections "Chess diagrams" and "Diagrams with no shorter realization".
Note that a tempo of 4 is impossible because any solution in p − 4 plies can be turned into 16 solutions in p plies with an initial knight dance, making the diagram not uniquely realizable in p plies. Perhaps surprisingly, some tempos larger than 4 plies are possible (but not multiples of 4). Click on a number in the table below to access a file with the diagrams.
| tempo 1 | tempo 2 | tempo 3 | tempo 5 | total | |
|---|---|---|---|---|---|
| ply 0 | 0 | 0 | 0 | 0 | 0 |
| ply 1 | 0 | 0 | 0 | 0 | 0 |
| ply 2 | 0 | 0 | 0 | 0 | 0 |
| ply 3 | 160 | 0 | 0 | 0 | 160 |
| ply 4 | 650 | 64 | 0 | 0 | 714 |
| ply 5 | 1786 | 136 | 0 | 0 | 1922 |
| ply 6 | 10663 | 418 | 0 | 0 | 11081 |
| ply 7 | 29731 | 788 | 0 | 0 | 30519 |
| ply 8 | 186637 | 3426 | 2 | 0 | 190065 |
| ply 9 | 966404 | 23492 | 634 | 0 | 990530 |
| ply 10 | 4719654 | 86281 | 501 | 13 | 4806449 |
| ply 11 | 22884520 | 264422 | 8060 | 24 | 23157026 |
Below are examples with large tempos constructed by people. As a bonus, starred (*) problems even have a unique solution in p − t plies.
| tempo 6 | tempo 7 | tempo 9 | |
|---|---|---|---|
| ply 20 | Michel Caillaud, 1996 (*) | ||
| ply 21 | Hiroshi Nagano, 1995 | ||
| ply 24 | Gerd Wilts, 2004 (*) | ||
| ply 26 | Michel Caillaud, 2000 (*) | Gerd Wilts, 1997 (*) |
More values of t (and even multiples of 4) can be obtained by changing the initial position (so-called A→B proof game problems). It is even possible to achieve every natural number starting with t=11 (so t=11,12,13,14,...) using the same pair of diagrams A & B.