Chess Problems by Computer
In December 2003, I wrote a program to search for chess games that are completely determined by the last move. Among other chess problems, the search uncovered this brain-teaser:
Black mates White on Black's 5th move by playing a rook, but the rook itself does not attack White's king. How did the game go? (the solution is unique)
Since then I improved my program and used it to search for other types of chess problems.
Chess problems
Chess statistics
As a byproduct of the searches, I also get some statistics on the first few plies.
Plot of chess statistics
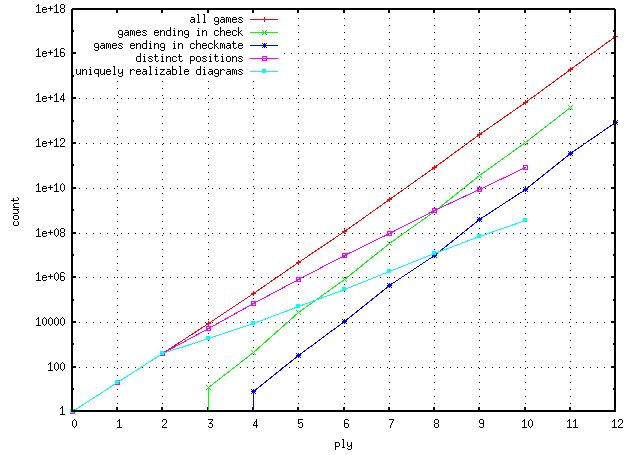
The curves "all games", "distinct positions", and "uniquely realizable diagrams" all start with the sequence 1,20,400 and eventually drop to zero.
- The number of chess games at ply n eventually drops to zero because of the 75-move rule, introduced on 1 July 2014. Without that rule, the number of chess games would be unbounded because the 50-move rule and the 3-fold repetition rule are not automatic, and the newly introduced 5-fold repetition rule, while automatic, only applies to consecutive repetition.
- The number of distinct positions at ply n eventually drops to zero because of the 75-move rule introduced on 1 July 2014. Without that rule the number would eventually cycle between the same four integers, each about half the total number of legal chess positions which is estimated to be between 10^43 and 10^47. The longest known dualistic proof game by L. Ceriani and
K. Fabel (1947) shows that at least one position is visited for the first time at ply 366.
- The number of uniquely realizable diagrams at ply n eventually drops to zero. The longest known dual-free proof game by D. Pronkin & A. Frolkin (1989) shows that it's non-zero at ply 115.
Articles
last updated: December 22, 2016

